Problem Set 3

The purpose of this problem set is for you to see how the ordinary least squares (OLS) estimator behaves under various assumptions in a linear regression model where you know what the model is – since you are going to be generating the data from a known data generating process (DGP).

The models estimated are simple bivariate regressions but the properties of the OLS estimator with vary with each case. This is demonstrated by changing the (a) distributional properties of the error term (variance-covariance structure), and (b) inducing correlation between the regressor and the error term. Any resulting bias and/or inconsistency will depend on the DGP.

To achieve certain results we will have to use a serially-correlated error structure, which is only appropriate in a time-series setting. For this reason, the models will be written with subscript \(t\) and not \(i\).

The code has been provided for model 1. You can then modify the code for models 2-4.

Preamble

You do not need to load data for this problem set.

clear 
//or, to remove all stored values (including macros, matrices, scalars, etc.) 
*clear all

* Replace $rootdir with the relevant path to on your local harddrive.
cd "$rootdir/problem-sets/ps-3"

cap log close
log using problem-set-3-log.txt, replace

However, since we are going to generate random variables, we should set a seed. This ensures replicability of the exercise. The number you choose is arbitrary, it simply ensures that any algorithms used to generate (pseudo) random variables start at the same place.

set seed 981836

Model 1: CLRM

This is your classical linear regression model. OLS estimator is unbiased and consistent.

\[ Y_t = \beta_1 + \beta_2X_t + \upsilon_t \qquad \text{with}\quad \upsilon_t\sim N(0,\sigma^2) \]

We know that the OLS estimator for \(\beta_2\) is given by,

\[ \begin{aligned} \hat{\beta}_2 =& \frac{\sum_t \big[(X_t-\bar{X})(Y_t-\bar{Y})\big]}{\sum_t (X_t-\bar{X})^2} \\ =& \beta_2 + \frac{\sum_t \big[(X_t-\bar{X})(\upsilon_t-\bar{\upsilon})\big]}{\sum_t (X_t-\bar{X})^2} \\ =& \beta_2 + \frac{\sum_t \tilde{X}_t\tilde{\upsilon}_t}{\sum_t \tilde{X}_t^2} \end{aligned} \] where \(\tilde{X}_t\) and \(\tilde{\upsilon}_t\) represent the demeaned counterparts of these variables. Alternatively, using linear algebra notation:

\[ \begin{aligned} \hat{\beta}_2 =& \frac{X'M_{\ell}Y}{X'M_{\ell}X} \\ =& \beta_2 + \frac{X'M_{\ell}\upsilon}{X'M_{\ell}X} \\ =& \beta_2 + \frac{\tilde{X}'\tilde{\upsilon}}{\tilde{X}'\tilde{X}} \end{aligned} \] where \(\tilde{X} = M_{\ell}X\), \(\tilde{\upsilon}= M_{\ell}\upsilon\), and \(M_{\ell} = I_n-\ell(\ell'\ell)^{-1}\ell'\) (the orthogonal projection of the constant regressor).

We know from Handouts 2 & 3,

\(E[\hat{\beta}_2] = \beta_2\) (i.e., unbiased)
\(p \lim \hat{\beta}_2 = \beta_2\) (i.e., consistent)

Can you demonstrate these results?

Simulation

Begin by designing a programme that takes the parameters of the model as arguments, generates the data, estimates the model, and then returns the stored values.

capture program drop mc1
program define mc1, rclass
    syntax [, obs(integer 1) s(real 1) b1(real 0) b2(real 0)  sigma(real 1)]
    drop _all
    set obs `obs'
    gen u = rnormal(0,`sigma')            // sigma is the std deviation of the error distribution
    gen x=uniform()*`s'                   // s is the std devation of the x distribution
    gen y=`b1'+`b2'*x + u                   // this generates the dep variable y
    reg y x
    return scalar b1=_b[_cons]            // intercept estimate
    return scalar b2=_b[x]                  // coeff on the x variable
    return scalar se2 = _se[x]            // std error
    return scalar t2 = _b[x]/_se[x]     // t ratio

end

Use the the simulate command in Stata to estimate the model 100 times:

simulate b1=r(b1) b2=r(b2) se2=r(se2) t2=r(t2), reps(100): mc1, obs(50) s(6) b1(4) b2(2) sigma(3)


      Command: mc1, obs(50) s(6) b1(4) b2(2) sigma(3)
           b1: r(b1)
           b2: r(b2)
          se2: r(se2)
           t2: r(t2)

Simulations (100): .........10.........20.........30.........40.........50.....
> ....60.........70.........80.........90.........100 done

Calculate the bias and plot the distribution of the bias.

gen bias2=b2-2
su b1 b2 se2 t2
su bias2
histogram bias2, normal xline(`r(mean)')


    Variable |        Obs        Mean    Std. dev.       Min        Max
-------------+---------------------------------------------------------
          b1 |        100    3.880226    .9977415   1.080851   6.090028
          b2 |        100    2.041985     .271704   1.365155   2.673303
         se2 |        100    .2520885    .0291596   .1814694   .3255497
          t2 |        100    8.216185      1.4968   5.484826   12.60699

    Variable |        Obs        Mean    Std. dev.       Min        Max
-------------+---------------------------------------------------------
       bias2 |        100    .0419852     .271704  -.6348448   .6733029
(bin=10, start=-.63484478, width=.13081477)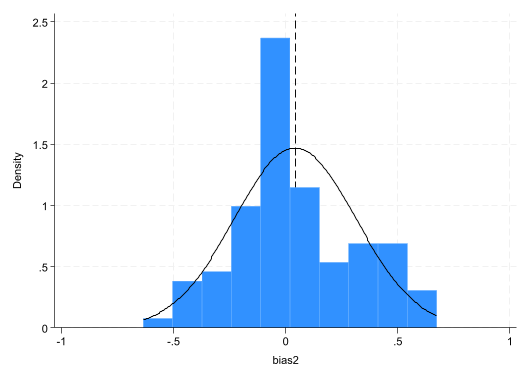

Model 2: Serial Correlation

Relax the assumption of an iid error term and allow for serial correlation. The OLS estimator is unbiased and consistent. However, the std errors are wrong since the software does not know that you have serially correlated errors and you are not taking this into account in the estimation.

\[ Y_t = \beta_1 + \beta_2X_t + \upsilon_t \qquad \text{where}\quad \upsilon_t = \rho \upsilon_{t-1}+\varepsilon_t \quad\text{and}\quad \varepsilon_t\sim N(0,\sigma^2) \] We say that \(U_t\) follows an AR(1) process. You can show that \(\hat{\beta}_2\) remains unbiased and consistant. However, the standard homoskedastic-variance estimator is incorrect:

\[ Var(\hat{\beta}_2) \neq \frac{\sigma^2}{Var(X_i)} \]

Simulation

You will need to redesign the above programme. The challenging part is the simulation of the error term. This needs to follow an AR(1) process and must therefore be generated in sequence. You can do this as follows:

  gen u=0 
    gen time=_n
    gen e = rnormal(0,`sigma')  
    forvalues i=2/`obs'  {
    replace u=`rho'*u[_n-1] + e if _n==`i'
    }

Model 3: Dynamic model without serial correlation

Consider a version of Model 1, where the regressor is the lag of the dependent variable. \[ Y_t = \beta_1 + \beta_2Y_{t-1} + \upsilon_t \qquad \text{with}\quad \upsilon_t\sim N(0,\sigma^2) \] The OLS estimator is now, \[ \hat{\beta}_2 = \beta_2 + \frac{\sum_t \tilde{Y}_{t-1}\tilde{\upsilon}_t}{\sum_t \tilde{Y}_{t-1}^2} \] This model is biased, since

\[ E\bigg[\frac{\sum_t \tilde{Y}_{t-1}\tilde{\upsilon}_t}{\sum_t \tilde{Y}_{t-1}^2}\bigg] \neq \frac{E\big[\sum_t \tilde{Y}_{t-1}\tilde{\upsilon}_t\big]}{E\big[\sum_t \tilde{Y}_{t-1}^2\big]} \] When the regressor was \(X_t\), the above statement was true given the Law of Iterated Expectations. However, you can use Slutsky’s theorem and the WLLN to show that \(\hat{\beta}_2\rightarrow_p \beta_2\). This result relies on the fact that \(Y_{t-1}\) is realized before \(\upsilon_t\) which is iid. Thus, the bias goes to 0 as \(n\rightarrow \infty\).

Simulation

You can use lag-operators in Stata to regress the outcome against its lagged value. For example:

    gen time=_n
    tsset time
    reg y  L.y

While the error term is serially uncorrelated (as in Model 1), you will need to generate the outcome sequentially (row value by row value). This is because the DGP has a lagged dependent variable structure.

Model 4: Dynamic model with serial correlation

Consider a version of Model 2, where the regressor is the lag of the dependent variable. \[ Y_t = \beta_1 + \beta_2Y_{t-1} + \upsilon_t \text{where}\quad \upsilon_t = \rho \upsilon_{t-1}+\varepsilon_t \quad\text{and}\quad \varepsilon_t\sim N(0,\sigma^2) \] As with model 3, the OLS estimator will be biased. In addition, since \(Cov(\upsilon_t,\upsilon_{t-1})\neq0\) and \(Cov(Y_t,\upsilon_{t})\neq 0\) (for any \(t\)), \[ \Rightarrow Cov(Y_{t-1},\upsilon_{t})\neq 0 \] As a result \(\hat{\beta}_2\) is inconsistent.

Simulation

You will need to use tricks from both models 2 and 3 to simulate this model.

Postamble

log close